Galerkin Neural Networks

Publications associated with this project:

Ainsworth, M., & Dong, J. (2021). Galerkin neural networks: A framework for approximating variational equations with error control. SIAM Journal on Scientific Computing, 43(4), A2474-A2501.
Ainsworth, M., & Dong, J. (2022). Galerkin neural network approximation of singularly-perturbed elliptic systems. Computer Methods in Applied Mechanics and Engineering, 402, 115169.
Howard, A., Dong, J., Patel, R., D’Elia, M., Stinis, P., & Maxey, M. (submitted 2023). Machine learning methods for particle stress development in suspension Poiseuille flows.

This project comprises the bulk of my Ph.D. research thus far. The motivation for this work was to address the gap between theoretical universal approximation results and the relatively low accuracy obtained for scientific computing applications in practice, largely due to stagnation in local minima because of highly nonconvex parameter landscapes.

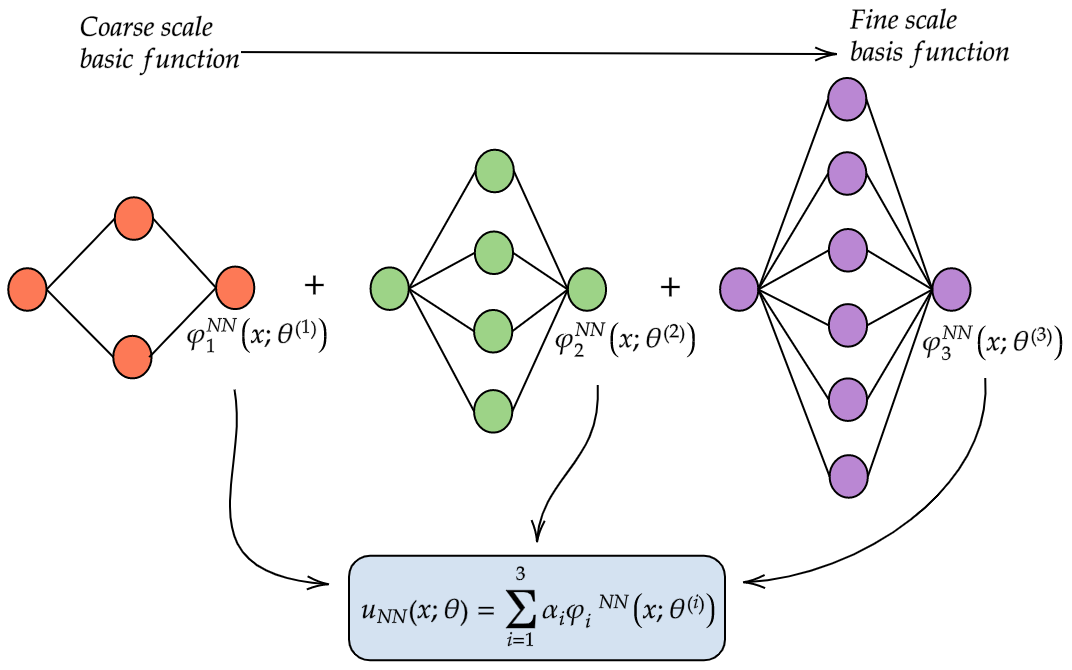
In this joint work with my advisor Mark Ainsworth, I developed the Galerkin neural network framework which allows us to approximate PDEs with rigorous control of the approximation error. At its heart, Galerkin neural networks is an approach which seeks to incrementally reduce the approximation error by decomposing the original problem into a sequence of smaller subproblems. These subproblems correspond to training very shallow networks which are easier to train.

We generate a sequence of basis functions corresponding to these networks which are then used to form a finite-dimensional subspace from which to approximate the variational form of a PDE. In particular given the problem

\[u \in X \;:\; a(u,v) = L(v) \;\;\;\forall v \in X,\]

and an initial approximation \(u_{0} \in X\), we compute the basis functions

\[\varphi_{i}^{NN} := \text{argmax}_{v \in V_{n}^{\sigma}} \frac{\langle r(u_{i-1}),v \rangle}{a(v,v)^{1/2}}\]

and solve

\[u_{i} \in S_{i} := \text{span}\{u_{0},\varphi_{1}^{NN},\dots,\varphi_{i}^{NN}\} \;\;:\;\; a(u_{i},v) = L(v) \;\;\;\forall v \in S_{i}.\]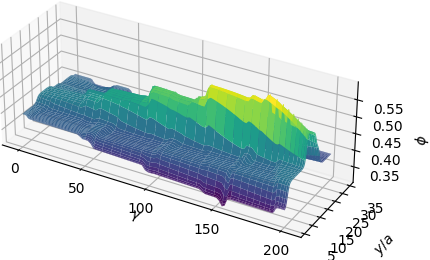

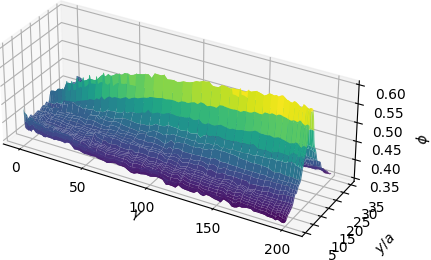
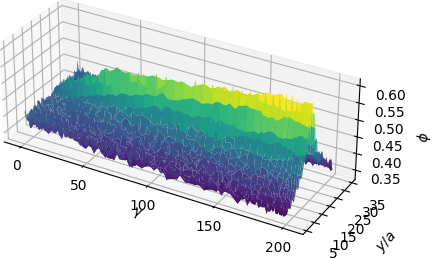
Figure: Incremental approximation of a function using one (left), three (middle), and seven (right) Galerkin neural network basis functions.

The basis functions are shown to be approximate Riesz representations of the weak residuals \(r(u_{i-1})\) and the approximation \(u_{i}\) is exponentially convergent with respect to the number of basis functions used in the subspace \(S_{i}\). Another attractive feature of the method is that the objective function used in training is shown to be an a posteriori estimator for the energy error.

Precise details can be found in the publications associated with this work above alongside a diverse array of numerical examples. In addition: