Three-phase Flow in Porous Media
high-order semi-implicit discretizations of three-phase flow
Publications associated with this project:
- Dong, J., & Rivière, B. (2016). A semi-implicit method for incompressible three-phase flow in porous media. Computational Geosciences, 20, 1169-1184.
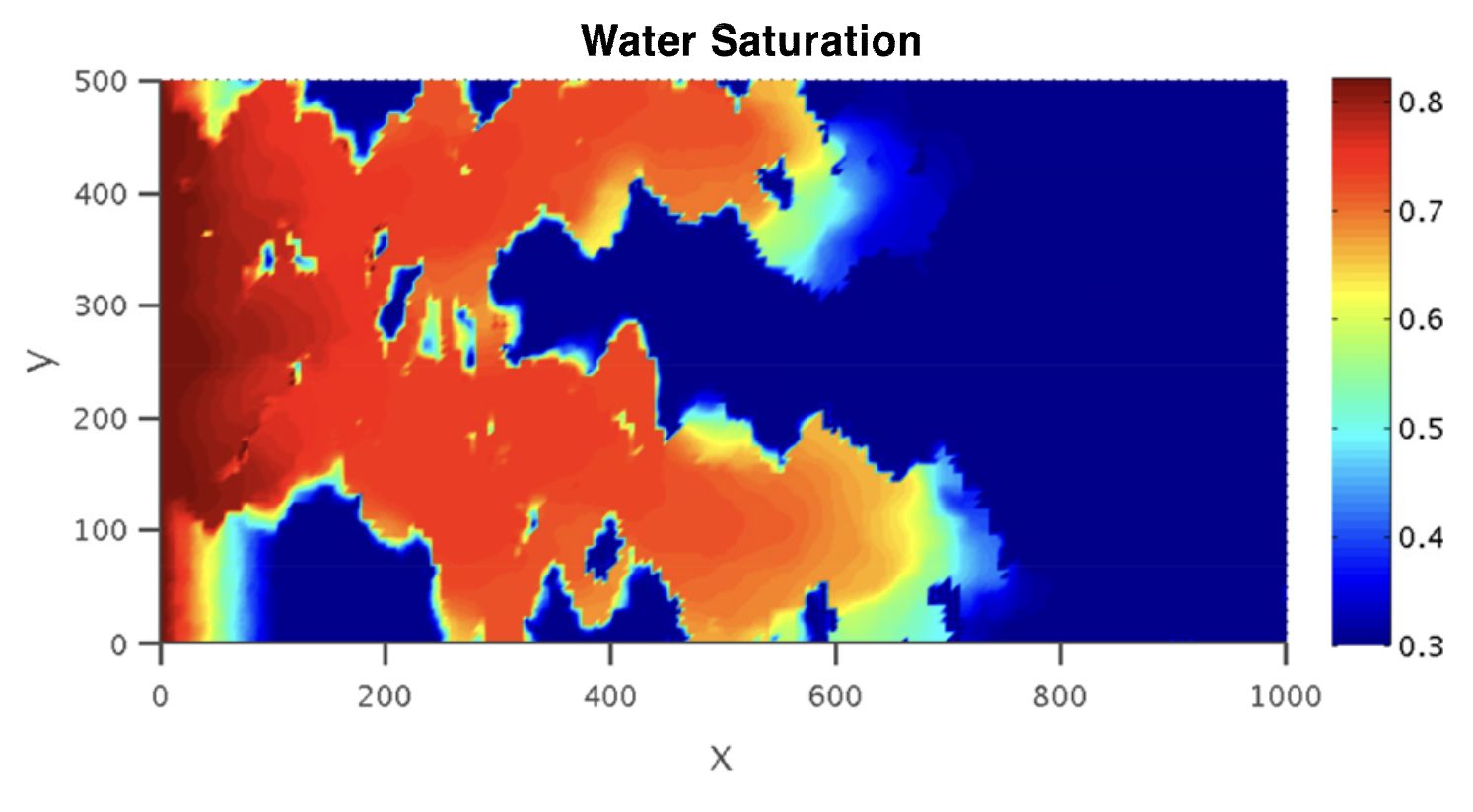
This project was carried out jointly with Beatrice Riviere during my time at Rice University. We considered a porous media \(\Omega \subset \mathbb{R}^{2}\) and the coupled nonlinear system
\[\begin{align} \begin{cases} -\nabla\cdot\left( h(s_{g},s_{w})\nabla p_{o} + f_{1}(s_{g},s_{w})\nabla s_{w} + g_{2}(s_{g},s_{w})\nabla s_{g} \right) = 0\notag\\ \dfrac{\partial(\phi s_{g})}{\partial t} + \nabla\cdot\left((f_{2}(s_{g},s_{w})\mathbf{u}) - g_{2}(s_{g},s_{w})\nabla s_{g}\right) = 0\notag\\ \dfrac{\partial(\phi s_{w})}{\partial t} + \nabla\cdot\left((f_{3}(s_{g},s_{w})\mathbf{u}) - g_{3}(s_{g},s_{w})\nabla s_{w}\right) = 0\notag\\ \end{cases} \end{align}\]with suitable boundary and initial conditions. The unknowns are the pressure \(p_{o}\) and saturations \(s_{w}\) and \(s_{g}\), where the subscripts denote different phases. The functions \(h, f_{i}, g_{i}\) are nonlinear functions of the saturations.
Due to the coupled nature of this system, implicit time-stepping schemes require the computation of a \(3\times 3\) Jacobian. Explicit schemes allow for complete decoupling but at the cost of much smaller time steps. In this work, we used a semi-implicit scheme which treats each equation as nonlinear in its primary variable (\(p_{o}\) in the first equation, \(s_{g}\) in the second, and \(s_{w}\) in the third). The nonprimary variables are evaluated at the previous time step.
The semi-implicit approach allows for larger time steps to be taken than in the explicit case while the smaller Jacobians are signficantly faster to compute.