Rayleigh-Taylor Instability (on GPUs)

HPC implementations of a discontinuous galerkin method for compressible Euler equations

This project was carried out jointly with Anna Lischke and was our final project for the graduate level course APMA 2822B: Parallel Computing on Heterogeneous (CPU+GPU) Systems. The focus of this project was to explore strategies for the parallelization of the Rayleigh-Taylor instability on both CPUs and GPUs. This problem is best described by the compressible Euler equations

\[\begin{align} \begin{cases} \dfrac{\partial\rho}{\partial t} + \dfrac{\partial(\rho u)}{\partial x} + \dfrac{\partial(\rho v)}{\partial y} = 0\\ \dfrac{\partial(\rho u)}{\partial t} + \dfrac{\partial(\rho u^{2} + p)}{\partial x} + \dfrac{\partial(\rho uv)}{\partial y} = 0\\ \dfrac{\partial(\rho v)}{\partial t} + \dfrac{\partial(\rho uv)}{\partial x} + \dfrac{\partial(\rho v^{2} + p)}{\partial y} = 0\\ \dfrac{\partial E}{\partial t} + \dfrac{\partial(u(E+p))}{\partial x} + \dfrac{\partial(v(E+p))}{\partial y} = 0 \end{cases} \;\;\;\text{in}\;\Omega \end{align}\]

with suitable boundary and initial conditions. The primary variables are the density \(\rho\), velocity \((u,v)\), and pressure \(p\). The internal energy \(E\) satisfies the relation \(E = p/(\gamma-1) + (u^{2}+v^{2})/2\).

The Rayleigh-Taylor instability arises when a fluid is suspended above another fluid of lower density. Velocity shearing causes instabilities to developo along the interface betweent the two fluids.

We discretize the equations in space using a modal discontinuous Galerkin method and in time using an explicit third-order Runge Kutta discretization. The explicit time-stepping scheme is easily parallelizable since it consists of vector additions and scalar-vector multiplications (although the size of the time step is limited by a CFL condition). The discontinuous Galerkin discretization contains boundary terms over the interfaces between elements which necessitates “communication” between neighboring elements. The benefit of the discontinuous Galerkin method is that the stencil of communication is compact and only involves immediate neighbors regardless of the order of polynomials used in the approximation. This is in marked contrast to high-order finite volume and difference schemes which require increasingly larger stencils as the order of the approximation is increased.

$$ \small \begin{array}{c|c|c|c} \textbf{DOFs} & \textbf{OpenMP} & \textbf{CUDA (1 GPU)} & \textbf{CUDA (2 GPU)}\\ \hline 2.3 \times 10^{6} & 126.2\text{m} & 12.6\text{m} & 6.5\text{m}\\ 9.4 \times 10^{6} & 1038.5\text{m} & 101.9\text{m} & 47.7\text{m}\\ 3.7 \times 10^{7} & - & 1032.7\text{m} & 367.7\text{m} \end{array} $$
Table: Wall times for several different meshes.

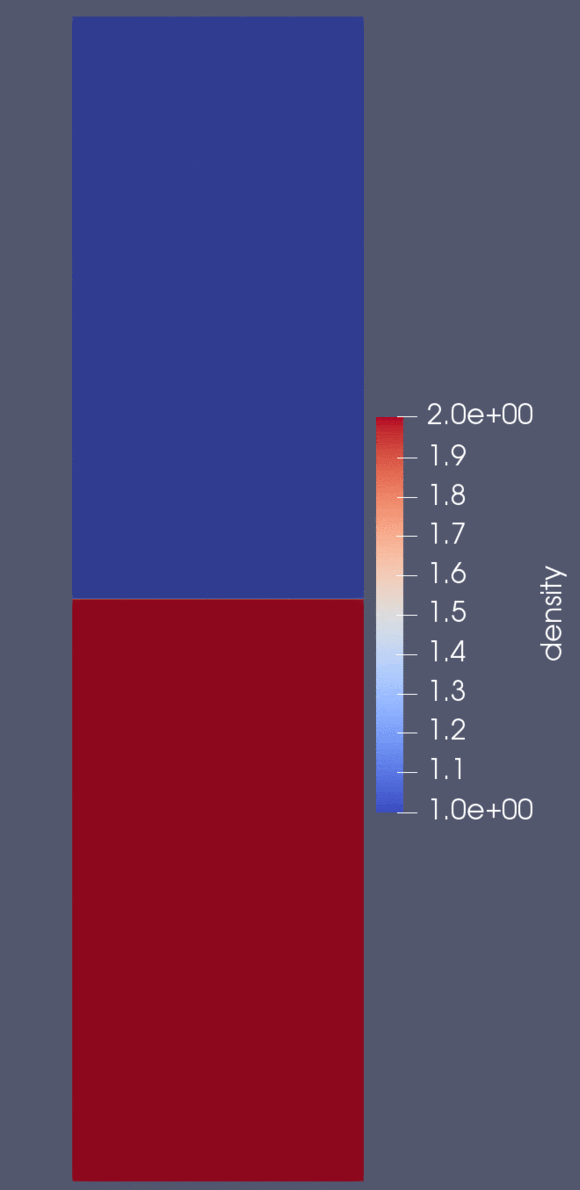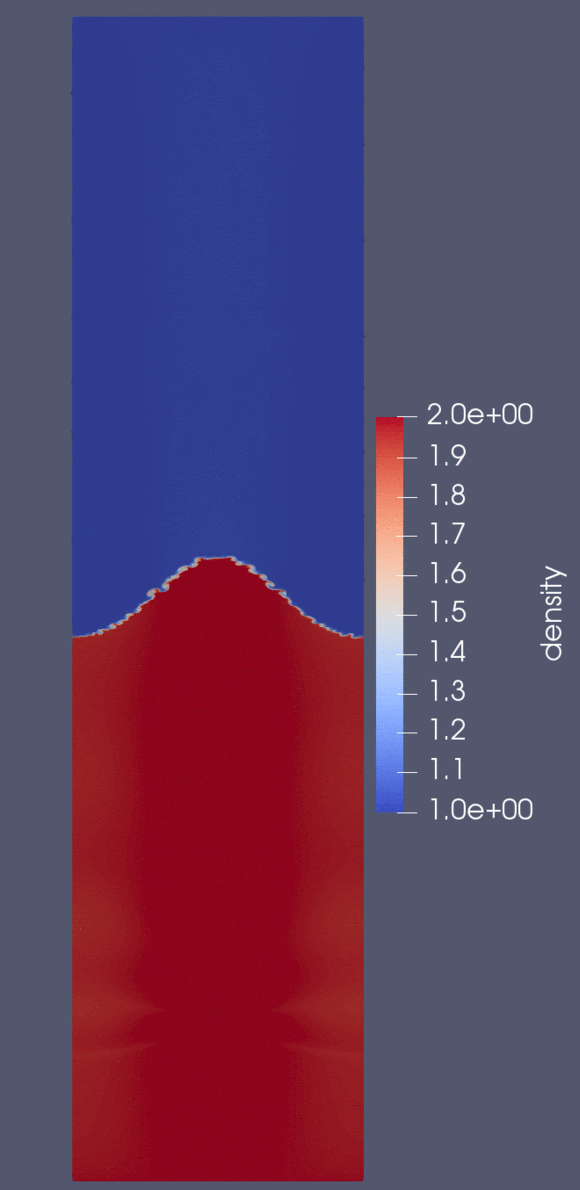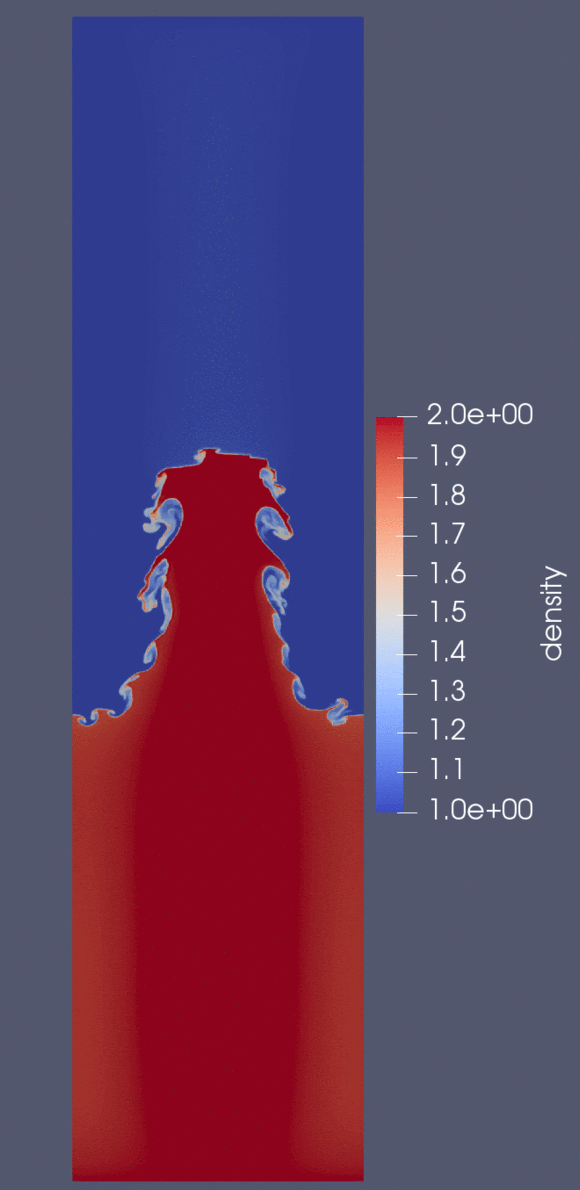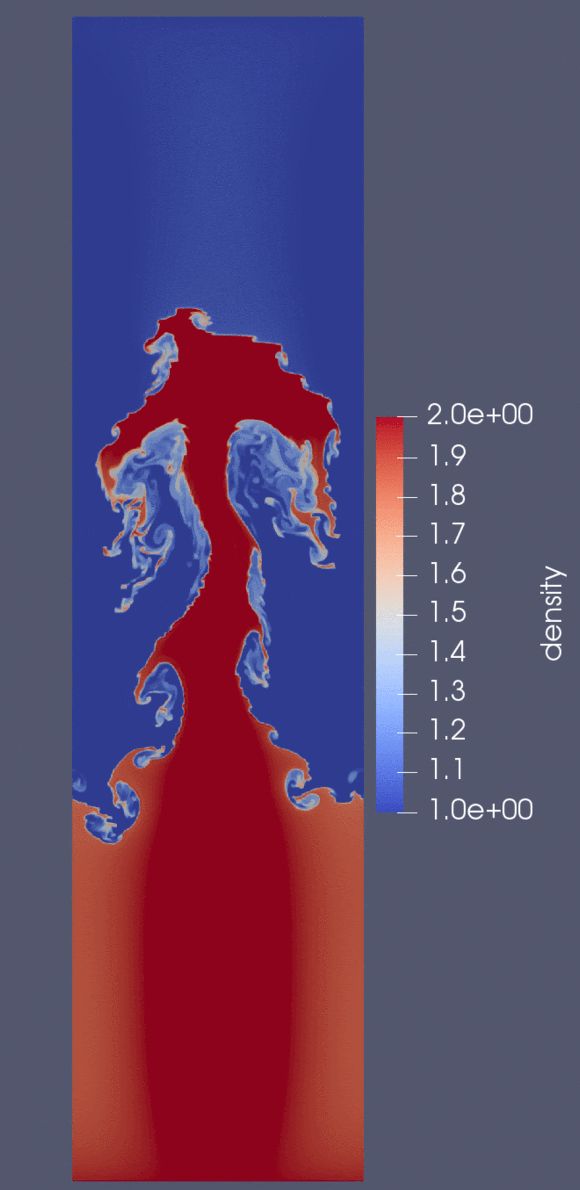
We compare CPU times with OpenMP and CUDA (with up to 2 GPUs (Tesla V100) and a simple domain decomposition). Materials for this project can be found below: